Baseline Model (기준모델)
예측 모델을 구체적으로 만들기 전에 가장 간단하면서도 직관적인, 최소한의 성능을 나타내는 기준이 되는 모델, 여기서는 평균값을 기준으로 사용하여 '평균기준모델'이라고 말할 수 있다. feature의 갯수와는 상관이 없음. 기준모델은 일반적으로 문제에 따라 다음과 같이 설정한다.
• 분류문제: 타겟의 최빈 클래스
• 회귀문제: 타겟의 평균값
• 시계열회귀문제: 이전 타임스탬프의 값
회귀 분석
단순 선형회귀분석이란 단일 독립변수에 대한 종속변수의 추이를 분석하는 것이다.
단순 선형회귀 모델
직선이므로 아래와 같은 식으로 표현할 수 있다.
이러한 형태의 식은 독립변수와 종속변수간의 관계를 설명해준다.

• 독립변수 (Independent Variable, x): 예측(predictor)변수, 설명(explanatory), 특성(feature)등
-> control, manipulate, change
• 종속변수 (Dependent Variable, y): 반응(response)변수, 레이블(label), 타겟(target) 등
-> outcome
• 회귀계수 α : 기울기 (Slope Coefficient)
-> 𝓍가 1만큼 변화했을때 y가 변화하는 정도가 얼마나 민감한지 나타낸다.
-> 기울기 B >A 의미는? x가 1만큼 변화했을 때 y의 변화하는 정도가 A보다 B가 더 민감하게 반응하다.
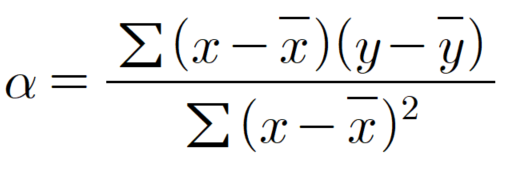
• 회귀계수 β : y 절편 (Intercept Coefficient)
-> 일반적인 경우 0이 될 수 없다. 웬만하면 반드시 존재함
![]()
1) the Best Fit 직선(=선형회귀 직선)은 어떻게 그릴 수 있을까?
• 선형회귀 직선? 잔차 제곱들의 합을 최소화 하는 직선이다.
• 잔차? 예측값과 관측값의 차이 = RSS = SSE ⬅ 회귀모델의 비용함수
• 예측값: 만들어진 모델이 추정하는 값
• 결국 머신러닝에서 '학습' 이란? 비용함수를 최소화하는 모델을 찾는 과정
[참고] 잔차와 오차는 다름.
오차(Error): 모집단에서 얻은 회귀식을 통해 예측한 값과 실제 관측한 값의 차이
잔차(Residual): 표본에서 얻은 회귀식을 통해 예측한 값과 실제 관측한 값의 차이
[참고] 비용함수와 손실함수는 엄밀히 말하면 다름.
비용함수(cost): 전체 데이터에 관한 손실. (손실을 모두 더한것이 비용 )
손실함수(loss): 데이터 딱 하나만에 해당하는 손실.
2) 잔차제곱합(RSS)을 최소화하는 방법 : 최소제곱법(OLS)
• 회귀계수 α, β => RSS를 최소화하는 값으로 모델 '학습'을 통해서 얻어지는 값
• 잔차제곱합 RSS : 예측한 값과 관측값의 차이(=잔차)를 제곱하여 합한 것.
-> 처음으로 돌아가서 이것을 최소화하는 직선이 단순 선형회귀 직선이 되는 것이다.

3) 정리해보면, 단순선형회귀 모델은?
1개의 '독립변수' 과 '종속변수'의 관계를 사용한 예측모델이다.
1개의 특성이 타겟에 미치는 인과관계를 분석하여 그 결과를 모델로 만들어 예측에 사용한다.
• 회귀선의 회귀계수는 2개: 기울기(Slope Coefficient), 절편(Intercept Coefficient)
• coefficient들을 어떻게 해석하느냐가 중요!
4) 회귀 분석 과정
step 1. 신뢰구간을 보고 의미가 있는지 없는지 먼저 확인.
▶첫번째 가설
H0: newspaper=0 뉴스페이퍼에 광고하는 것은 세일즈에 미치는 영향이 없다.
Ha: newspaper!=0 뉴스페이퍼에 광고하는 것은 세일즈에 미치는 영향이 있다.
뉴스페이퍼(feature)가 세일즈(target)와의 관계를 알아보기 위해 단순선형회귀모델을 돌렸을 때 p-value 가 0.7 나오므로 귀무가설을 기각할 수 없다. 즉, 뉴스페이퍼가 세일즈에 미치는 영향이 없다고 볼수 있음.
▶ 두번째 가설
H0: radio=0 라디오에 광고하는 것은 세일즈에 미치는 영향이 없다.
Ha: radio!=0 라디오에 광고하는 것은 세일즈에 미치는 영향이 있다.
라디오(feature)가 세일즈(target)와의 관계를 알아보기위해 단순선형회귀모델을 돌렸을 때 p-value 가 0.0000002나오므로 귀무가설을 기각한다. 즉, 라디오에 광고하는 것은 세일즈에 영향을 미친다.
step 2. 의미있는 feature를 찾았다면? 회귀계수를 해석하여 얼마나 영향이 있을지 확인.
라디오의 estimate 0.188 ? 상대적으로 라디오에 광고를 하나씩 늘릴때마다 0.188만큼 sales가 증가할 것이다.
Intercept ? 아무 매체에도 광고하지 않았을때 sales양: 300
=> radio에 광고했을때 sales양: 300+18.8
OLS에 대해
• 최소자승법(Ordinary Least Squares)은 잔차제곱합(RSS: Residual Sum of Squares)을 최소화하는 벡터를 구하는 방법이다.
• 분포되어 있는 데이터의 추세선을 그리고자 할 때 주로 사용된다.
• 추세선과 데이터 벡터의 오차는 다양한 형태로 표현될 수 있지만 가장 보편적이고 쉽게 이해할 수 있는 지표는 잔차 제곱합이다.
• 우리가 오늘 배웠던 단순선형회귀로만 제한하여 생각해 보자. 그리고 어떤 데이터값의 벡터가 (xi,yi) 이고, 단순회귀선의 식이 yi^=axi+b 라고 가정해보자.
• 이때, x1에 따른 y1^과 실제 y1의 값은 동일하지 않다.
• 모든 데이터를 지나도록 일차방정식 선을 그릴 수 있으면 좋겠지만, y1^≠y1인 것 처럼, 단순 선형회귀분석으로는 불가능 한 일이다.
• 따라서 (xi, yi) 에서 y^=ax+b 까지의 거리, 즉 오차를 최소화 할 수 있는 방법을 사용하여 데이터의 분포를 가장 잘 반영하는 직선(회귀선)을 그리는 것으로 최선의 타협을 한다.
• 여기서 해당 오차를 최소화 하는 방법 중 하나가 잔차제곱합을 최소화하는 최소자승법이다.
[참고자료]
https://knowing207.tistory.com/20
Chapter 3. 선형회귀 (Linear Regression) - 1) 단순선형회귀
** 단순선형회귀 파트에서는 ISLR 교재 내용을 기반으로 아래 블로그 참고하여 내용을 정리했습니다. 개념, 이론 https://m.blog.naver.com/jhkang8420/221291682151 수학적 증명 https://rpubs.com/Jay2548/519..
knowing207.tistory.com
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=dhkdwnddml&logNo=220156712894
[#2]계량경제학 OLS method, 최소자승법
회귀분석을 할 때, 가장 간단한 관계식을 한 번 추정해보도록 하겠습니다. (▲True model) 만약 Y와 X의...
blog.naver.com
'코드스테이츠 AI 부트캠프 > Section 2' 카테고리의 다른 글
| AIB_234_복습정리 : PDP, SHAP (0) | 2021.12.04 |
|---|---|
| AIB_231_복습정리 : 불균형 클래스 (0) | 2021.12.04 |
| [비공개] AIB_222_복습정리 : Random Forests, Hyper parameter tuning (0) | 2021.12.04 |
| [비공개] AIB_221_복습정리 : Decision Trees (0) | 2021.12.04 |
| AIB_212_복습정리 : Multiple Linear Regression / Bias-Variance Trade off (0) | 2021.12.04 |