단순 선형회귀 모델
: 특성이 하나뿐인 선형회귀 모델
▶ 2차원 직선

다중 선형회귀 모델
: 특성이 여러개인 선형회귀 모델 (하나의 특성만으로된 모델로는 데이터들을 설명할 수 없는 경우)
▶ 특성의 갯수만큼 차원이 늘어남.

• 다중선형회귀 모델은 여러개의 독립변수와 한개의 종속변수와의 관계(독립변수들이 종속변수에 미치는 영향 즉 인과관계를 분석)를 사용하여 예측하는 모델이다.
• 사실상 특성이 3개 이상이 되어 4차원을 넘어서는 순간부터 직관적 이해가 불가능
• 분석 그래프의 차원이 증가하면 계산이 복잡해질뿐만아니라 '다중공선성', '과적합', 차원의저주' 등과 같은 문제가 발생하기도 한다. 이런 부수적인 문제들까지도 고려를 해야하는 모델이다.
• 식 (2)에서 회귀계수는 단순회귀모형에서처럼 독립변수와 종속변수의 선형적 관계를 보여준다. 다만 단순회귀모형에서와 달리 다중회귀모형의 회귀계수는 회귀모형에 포함된 다른 독립변수들을 통제한 상태에서 특정 독립변수와 종속변수의 선형적 관계를 나타낸다.
• 평가지표로는 RMSE가 많이 쓰임. MAE는 많이 안쓰임
[참고] 다중 선형회귀 vs. 다항 회귀(Polynomial regression)
- 곡선 형태로, 선형 모델의 한계를 어느 정도 극복할 수 있다.
회귀 모형 해석(평가방법)
- 회귀 모형이 통계적으로 유의미한지: F통계량과 유의확률로 확인
- 회귀 계수들이 유의미한지: 회귀계수의 t값과 유의확률로 확인
- 원천 자료에 대한 회귀모형의 설명력: 결정계수(R-square) 확인
- 모형이 데이터에 잘 적합한지: 잔차 통계량 확인, 회귀진단 진행(선형성~정상성)
다중공선성 이란?
다중 선형회귀 모델에서 설명변수 사이에 강한 상관관계가 존재하는 것을 말한다.
- 반응변수(타겟): 집 값
- 설명변수(피쳐): 방의 개수, 화장실 개수
예를 들어 생각해보자. 위 두 피쳐의 관계를 보니, 방의 갯수가 많아지면 화장실갯수가 많아지는 '선형' 의 상관관계가 있음을 발견했다고 하자. 이것은 두 피쳐간 서로 독립적이지 않고 다중공선성이 존재한다고 말할 수 있다. 이렇게 다중공선성이 있는 두 피쳐를 넣고 다중 선형회귀 분석을 하면 부정확한 회귀계수가 나오면서 회귀 결과를 왜곡할 수 있다. 하나의 계수는 +에 하나의 계수는 -로 반대로 나옴. 다중공선성 확인 및 사전 처리를 미리 하지않고 바로 회귀분석을 했는데 이렇게 다르게 나온다면 다중공선성이 있는 두 변수를 채택했을 가능성이 있을 수 있다.
다중공선성을 확인하는 방법?
1. 산점도로 시각화해서 선형의 강한 상관관계가 있는지 대략적인 파악 가능
2. 상관관계 분석을 통해 상관관계 확인하기
3. 회귀분석의 공선성 VIF(분산팽창짖수) 계산하여 확인하기
다중공선성을 해결하는 방법?
1. 두 변수 중 하나 제거
2. 제거시 R^2유지되는 변수를 제거
=> 다중공선성을 가진 변수는 혼자 존재하지 않는다. 만약 A, B, C, D 피쳐가 4개인 데이터에 대해 VIF를 계산했는데, A의 VIF가 10보다 크다면, 반드시 B, C, D 중에서도 VIF가 10보다 큰 변수가 존재한다.
다중공선성에 대해 생각할 때 주의해야할 점
다중공선성이 있다면 상관관계가 높지만, 상관관계가 높다고 반드시 다중공선성이 있는 것은 아니다.
데이터의 수가 적은 경우, 변수간 상관관계가 높아서 다중공선성이 없을 수도 있다.
다중공선성이 높으면 예측값의 신뢰구간이 넓게 형성되는 현상을 갖는다.
Overfitted vs Underfitted (과적합 vs 과소적합)

[그림 - 좌] 과소적합된 모델
선형으로 예측했을때 훈련데이터와 차이가 많이 난다. 훈련데이터의 일반화 성질조차 학습도 못한거.
[그림 - 중] 세개의 그림중에 가장 좋은 모델
어느 정도 훈련데이터의 패턴도 잡아내면서 bias, variance도 적당.
[그림 - 우] 과적합된 모델
훈련데이터에서의 모든 패턴을 잡아내어 학습이 잘 된것처럼 보이나, 과하게 너무 딱 맞아서 오히려 테스트데이터에서 일반화가 안되는거.
(차수가 높은 함수 그래프로 생각)

Bias-Variance Trade-off (편향 - 분산 트레이드오프)
High Bias (편향 ⬆) ---> 과소적합 상태
High Variance (분산 ⬆) ---> 과적합 상태
• 분산 에러가 높은 경우 과대적합(overfitting), 편향 에러가 높은 경우 과소적합(underfitting)
• 훈련 데이터에 모델이 과대적합(overfitting)될 경우 모델의 편향 에러는 작아지지만 테스트 데이터에서의 성능을 떨어져 분산 에러는 커질 수 있고, 반대로 훈련 데이터에 과소적합(underfitting)될 경우 모델의 편향 에러는 커지지만 테스트 데이터에서의 성능은 유지되어 분산 에러는 작아질 수 있다. 즉, 머신러닝 모델링에서 편향 에러를 줄이려하면 분산 에러가 커지고, 분산 에러를 줄이려 하면 편향 에러가 커지는 관계를 보이는데 이러한 현상을 '분산-편향 Trade-Off'라고 한다.
• 편향 에러와 분산 에러가 모두 높은 경우 학습 데이터에서도 학습이 충분히 되지 않았다는 의미이고, 테스트 데이터에서도 성능이 안 나오는 모델이라는 의미다.
• 편향 에러와 분산 에러가 모두 낮은 경우 학습 데이터에서도 학습이 충분히 되었고, 테스트 데이터에서도 성능이 잘 나오는 모델이라는 의미다.
• 훈련 데이터에서의 성능과 테스트 데이터에서의 성능이 유사하게 나온 것을 '일반화(Generalization)'가 잘 된 모델이라고 한다.
▶ 모델을 만들 때 bias 와 variance를 동시에 줄일 수 있으면 좋겠지만 하나를 포기해야한다면, bias를 줄이는 것 보다 variance를 최소로 하는 모델을 만들면 어떨까? 즉 과적합 방지에 중점을 두면 어떨까? (다음 노트 이어서)
▶ bias가 증가되더라도 variance 감소폭이 더 크면 expected MSE는 감소. 즉 예측 성능 증가.
Bias : 훈련 데이터셋의 오차
Variance : 테스트 데이터셋의 오차
오차에 패턴이 있다는거는 모델이 제 역할을 잘 하지 못했다.
오차에 패턴이 없어야 모델이 다 잘 잡아줬다는 것이다.
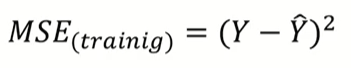

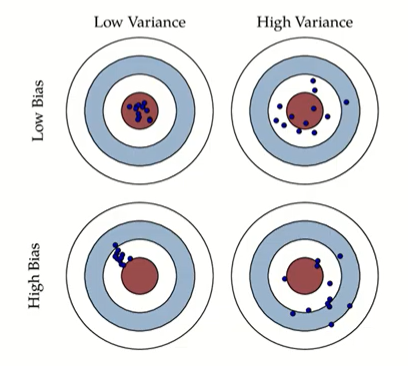
빨간색 과녁 : Target
파란색 점들 : X_test data
1. 파란색 점들이 빨간색 과녁 안에 들어가서 모여있다
: 모델에 X_test data를 넣었더니 target을 잘 맞췄다. -> best model
2. 파란색 점들이 빨간색 과녁 주변에 흩어져있다.
: 모델에 X_test data를 넣었더니 target을 잘 맞추지 못했다. -> 모델이 과적합되어 일반화되지 못함 (high variance)
3. 파란색 점들이 모여있지만, 빨간색 과녁을 빗나갔다.
: 모델에 X_test data를 넣었더니 target을 하나도 맞추지 못했다. -> 모델이 과소적합되어 일반화할 수 없음 (high bias)
4. 엉망진창
[참고자료]
앎이의 데이터분석 Note 블로그: 다중선형 회귀 (https://knowing207.tistory.com/21)
정보사회학연구소 웹사이트: 표와 그래프(5) 다중회귀분석 (http://piramvill2.org/?p=3137)
Must Learning with R 위키독스: 다항회귀분석 (https://wikidocs.net/73484)
이냥저냥 블로그: 회귀분석 성능 평가법 (https://blog.naver.com/choheeee22/222473090839)
예제와 함께하는 쉬운 통계 블로그: 상관계수와 결정계수 (https://m.blog.naver.com/istech7/50153288534)
s5unnyjjj님 블로그: 일반화, 과소적합, 과대적합, 편향, 분산 (https://s5unnyjjj.tistory.com/41)
YSY의 데이터분석 블로그: 회귀분석 실습(4) 다중공선성 python (https://ysyblog.tistory.com/122)
'코드스테이츠 AI 부트캠프 > Section 2' 카테고리의 다른 글
| AIB_234_복습정리 : PDP, SHAP (0) | 2021.12.04 |
|---|---|
| AIB_231_복습정리 : 불균형 클래스 (0) | 2021.12.04 |
| [비공개] AIB_222_복습정리 : Random Forests, Hyper parameter tuning (0) | 2021.12.04 |
| [비공개] AIB_221_복습정리 : Decision Trees (0) | 2021.12.04 |
| AIB_211_복습정리 : Simple Linear Regression (0) | 2021.12.04 |