표본 분산을 떠올려보자.

표본 분산은 간단하게 위와 같이 쓸 수 있지만, 아래와 같이 표본에서 관측값이 차지하는 비율(=상대도수)을 사용하여 쓸 수도 있다. 왜냐하면 표본 평균은 '관측값 x 상대도수'의 합계로 나타낼 수 있다고 했고, 표본 분산은 편차제곱을 평균낸 것이므로 이를 '편차제곱 x 상대도수'의 합계로 나타낼 수 있는 것! 예를 들어 n이 10이라고 하면 아래와 같이 나타낼 수 있다.


✓ n이 계속 커지면 '표본'은 결국 '모집단'이 되고, 특정 값에 대한 '비율'은 특정 값이 발생할 '확률'이 된다. 이에 따라 표본 평균은 모평균이 되며 표본 분산은 모분산이 된다.
• 표본 → 모집단
• 표본에서 특정 값에 대한 비율 → 사건이 일어날 '확률'
• 표본 평균 → 모평균
• 표본 분산 → 모분산
• n/(n-1) → 1
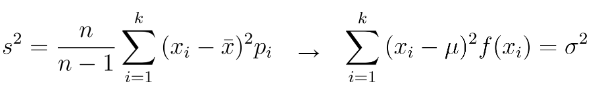
모분산 = 확률변수의 분산
• 모분산은 확률변수의 분산으로 표현할 수 있다.
(1) 이산 확률변수의 분산

(2) 연속 확률변수의 분산

모집단의 표준편차 = 확률변수의 표준편차

확률변수의 분산, 표준편차 성질

위치의 변화를 주는 상수 b는 분산에 영향을 주지 않는다. 분산은 측정단위의 제곱의 형태로 나타낸 것이기 때문에 a는 제곱하여 곱해주는 것이다.
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 통계적 추론 (0) | 2022.08.23 |
|---|---|
| 기초통계 / 이산형 확률분포 (1) 베르누이 분포, 이항 분포 (0) | 2022.08.18 |
| 기초통계 / 확률변수의 기대값 (0) | 2022.08.18 |
| 기초통계 / 확률 변수, 확률 분포 (0) | 2022.08.16 |
| 기초통계 / 표본 공분산, 표본 상관계수 (0) | 2022.08.15 |