이산형 확률분포
- 베르누이 분포
- 이항 분포
- 기하 분포
- 포아송 분포
✔️ 이산 확률분포는 확률질량함수를 이용하여 표현한다.
✔️ 확률질량함수란? 이산 확률변수가 특정 값을 가질 확률을 나타내는 함수다.
베르누이 분포
1) 베르누이 시행
① 각 시행의 결과가 두 가지만 있는 실험. (성공/실패, 앞/뒤 ...)
② 각 시행이 독립적으로 수행.
③ 모든 시행에서 결과의 확률은 항상 동일.
• P(성공) = P(S) = p
• P(실패) = P(F) = 1 - p = q
⇒ 이항분포, 음이항분포, 다항분포의 기본이 되는 개념.
2) 베르누이 확률 분포
모수(성공할 확률)이 p인 베르누이 시행으로 인해 확률변수가 1(성공)과 0(실패)의 값을 갖는 확률분포. 확률변수 X가 베르누이 확률변수라면 아래와 같이 표시할 수 있다.

3) 베르누이 확률 분포의 확률질량함수

4) 베르누이 확률 변수의 기대값과 분산
기대값

분산

이항 분포(Binomial distribution)
성공할 확률이 p인 베르누이 시행을 n번 반복했을 때, 성공횟수를 확률변수로 갖는 분포.



1) 이항 확률 변수의 기대값과 분산
베르누이 확률 변수의 기대값을 이용하여 구할 수 있다.
기대값

분산

2) 이항 분포의 확률질량함수

• 성공할 확률이 p, 시행횟수 n번인 이항 분포의 확률질량함수는 위와 같이 쓴다.
• n과 p에 따라 확률이 달라지게 되므로, 결국 n과 p가 이항분포 모양을 결정한다고 할 수 있다. 이처럼 분포의 특성을 완전히 결정하는 값을 모수(parameter)라고 한다.
• 확률변수 X가 이항 확률변수라면 아래와 같이 표시할 수 있다.
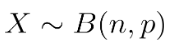
예시
X: 주사위를 세번 던져서 6이 나온 횟수
(시행 결과가 6이 나오거나 안나오거나 두 개 이고, 각각의 시행이 독립이므로 이는 베르누이 시행을 3번한 것과 같다)
<베르누이 시행>

<베르누이 시행 3번>
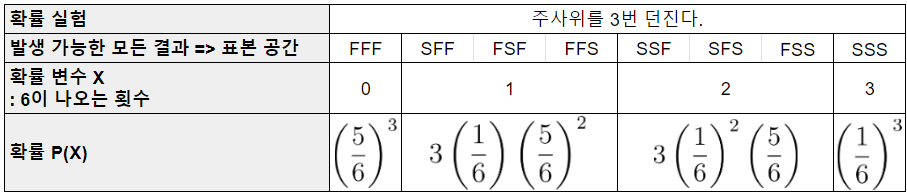
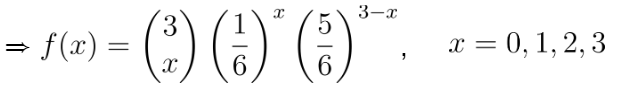
예시
윷이 젖혀질 확률: p = 0.4
X: 대한이가 윷을 4번 던져서 윷이 젖혀진 횟수
Y: 민국이가 윷을 6번 던져서 윷이 젖혀진 횟수
이때, 두 사람이 던진 윷 중에서 젖혀진 윷이 2개 이하일 확률은?
X ~ B(4, 0.4) ⇒ 성공할 확률 p = 0.4 인 베르누이 시행을 4번한 것.
Y ~ B(6, 0.4) ⇒ 성공할 확률 p = 0.4 인 베르누이 시행을 6번한 것.
그러므로 X+Y ~ B(10, 0.4) 이렇게 쓸 수 있다.
P(X+Y ≤ 2)
= P(X+Y = 2) + P(X+Y = 1) + P(X+Y = 0)
= ₁₀C₂(0.4)²(0.6)¹⁰⁻² + ₁₀C₁(0.4)¹(0.6)¹⁰⁻¹ + ₁₀C₀(0.4)⁰(0.6)¹⁰⁻⁰
= 0.167
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 표본 추출 시, 가중치 조정이란? (0) | 2024.02.14 |
|---|---|
| 기초통계 / 통계적 추론 (0) | 2022.08.23 |
| 기초통계 / 확률변수의 분산과 표준편차 (0) | 2022.08.18 |
| 기초통계 / 확률변수의 기대값 (0) | 2022.08.18 |
| 기초통계 / 확률 변수, 확률 분포 (0) | 2022.08.16 |