확률 현상
① 발생 가능한 모든 결과들에 대해 알고 있지만,
② 어떤 결과가 나올지 모르는 현상 → 불확실성
주사위를 던질때 나오는 숫자의 가능한 결과는 {1,2,3,4,5,6} 중에서 하나임을 알고 있지만, 그중에서 실제로 어떤 결과가 나올지는 정확히 알 수 없다. 이것을 확률 현상이라고 말한다.
1.확률 실험(random experiment)
- 발생 가능한 모든 결과의 집합을 알고 있지만 실제로 어떤 결과가 나올지 모르는 현상에 대해, 동일한 조건으로 여러 번 실험을 반복하며 결과를 관찰하는 과정.
- 왜 할까? 확률 실험은 확률을 추정하기 위한 근거를 마련하는 과정으로 볼 수 있다.
❓확률 실험 vs. 시행(trial)
- 확률 실험과 시행은 둘다 확률 현상에 기인하여 행해지는 것이기때문에 같은 의미로 사용될 수도 있다. 하지만 시행과 실험의 정의를 정확히 구별하자면, 확률 실험은 여러 시행의 조합으로 형성된 더 큰 실체로 생각할 수 있다.
- 노랑공 3개, 파랑공 7개가 들어있는 주머니에서 3개의 공을 뽑는 확률 실험에서, 한번에 하나씩 뽑는 총 3번의 시행을 할 수 있다. 따라서 확률 실험에 여러 번의 시행이 포함될 수 있는 것이다.
2. 표본공간(sample space)
- 확률 실험에서 발생 가능한 모든 결과들의 집합
3. 사건(event)
- 표본공간 내에서의 관심을 가지는 부분집합
4. 확률(probability)
- 어떠한 사건이 일어날 가능성이 얼마나 되는지 [0, 1]로 나타내는 측도
- 즉, 확률 실험에서 관찰된 결과를 통해 이 사건이 일어날 객관적인 가능성을 0과 1 사이의 숫자로 정량화하여 추정하는 것
- 확률을 알기 위해서는 '확률 실험'이 전제되어야 하고, '확률 실험'을 하려면 '표본 공간'과 '사건'이 정해져야 한다.
- 확률은 모집단이 어떤 형태로 이루어져 있는지를 보여주는 것이다. 이렇게 해석하는 것을 통계적 확률이라고 한다.
상대도수 극한의 개념을 이용한 '통계적 확률'의 이해
- 사건 A: 동전을 던졌을 때 앞면이 나올 확률은?
- 동전을 n번 던져서 앞면이 나온 횟수를 n(A) 라고 하면, 앞면이 나온 비율(=상대도수)은 n(A)/n 이다.
- 만약 확률 실험을 무한히 반복한다면 n(A)/n 은 어떤 특정 값으로 수렴하게 된다.
- 즉 확률 실험을 무한히 반복하면 상대도수가 어떤 특정 값으로 수렴하는데, 이 값이 사건 A가 일어날 확률이다. ⇒ '상대도수 극한의 개념'

정리해보면
n번의 실험을 통해 발생한 결과는 n개의 표본을 의미하는 것이므로, n번의 실험을 무한히 반복한다는 것은 표본을 점점 많이 뽑다보면 결국은 모집단이 된다는 것임을 의미한다(상대도수 극한의 개념). 결과적으로 "확률은 표본에 관한 것이 아니라, 모집단이 어떤 형태로 구성되어 있는지를 보여주는 것이다." 라고 해석할 수 있고, 이것을 우리는 통계적 확률이라고 한다.
확률 변수 (random variable)
확률 실험에 대하여 표본공간의 값들을 어떤 숫자로 나타내는 것을 확률 변수라고 한다. 그 숫자는 확률에 따라 정해지는 값이므로 변수라고 할 수 있다. 정의역이 표본공간, 공역이 실수인 함수의 형태로 표현된다.
불확실성을 가지는 사회적, 자연적 확률 현상을 일종의 확률 실험으로 이해하고, 이에 대해서 표본공간의 값들을 확률 변수 즉 숫자로 나타냄으로써 불확실한 현상을 수학적으로 모형화하는 것이다. 불확실성을 제거하는 것이 아님을 주의하자! 이를 통해 구체적으로 계량화된 분석을 할 수 있다. 확률 변수는 대문자 X, Y, Z 등으로 표시하고, 확률 변수의 값은 소문자 x, y, z 등으로 표시한다.
예시
"주사위를 한번 던졌을 때 6이 나올 확률을 구해보자(확률 = 사건이 발생할 객관적인 가능성)."
- 주사위 1번 던지기 ⇒ 시행이 단 1번인 '확률 실험'
- 주사위를 1번 던졌을 때 6이 나오는 횟수 ⇒ 확률 변수 X
- 한번 던졌을 때 6이 나올 수도 있고 안나올 수도 있으니까, 확률 변수 X가 가질 수 있는 값은 {0, 1}이다.
- 5/6 확률로 0 값을, 1/6 확률로 1 값을 취할 수 있다.
| 확률 변수 X : 6이 나오는 횟수 |
발생 가능한 결과 집합 | 발생 가능한 결과 수 | 확률 P(X) = 사건 수/6 |
| X=0 (6이 0회 나옴) | {1, 2, 3, 4, 5} | 5개 | P(X=0) = 5/6 ≈ 0.833 |
| X=1 (6이 1회 나옴) | {6} | 1개 | P(X=1) = 1/6 ≈ 0.167 |
| 총합 | 6개 | 1 |
- 이 표는 이산형 확률분포의 확률분포표로 볼 수 있음.
- 이 분포는 이산형 확률분포 중 베르누이 분포(Bernoulli Distribution)에 해당하며, 베르누이 분포의 가장 기본적인 형태.
확률 변수의 종류
이산형 확률 변수: 확률 변수 X가 취할 수 있는 값들이 유한이거나 셀 수 있을 경우
연속형 확률 변수: 확률 변수 X가 취할 수 있는 값들의 집합이 실수의 구간을 이루어 셀 수 없을 경우
확률 분포 (probability distribution)
정의
- 확률 분포는 특정 사건에 대해 확률 변수가 가질 수 있는 모든 값과 그 값을 가질 확률을 짝지어 놓은 것이다.
- 결국, 확률 분포는 모집단에 있는 모든 가능한 값과 그 값들이 얼마나 자주 나타나는지(=확률) 표현한 것이다.
- 즉 확률 분포를 보면 특정 사전에 대한 확률들이 어떤 형태로 분포되어 있는지 알 수 있는데, 이는 확률 분포를 통해 모집단이 어떤 형태(분포)로 이루어져 있는지 알 수 있다는 말이다. (표본에 관한 것이 아님!)
확률 분포는 언제 필요할까?
- 단순히 특정 사건이 발생할 확률만 궁금할 때는 '해당 사건의 경우의 수'와 '전체 표본 공간의 경우의 수'만 알면 됨. 확률 분포가 필요하지 않음. (예를 들어 주사위를 한 번 던져 '6이 나올 확률'이 궁금하다면, 1/6이라는 하나의 값만 계산하면 된다. {1, 2, 3, 4, 5, 6}의 모든 확률을 다 계산할 필요는 없음)
- 확률 분포는 단순한 개별 확률을 넘어, 확률 변수가 가질 수 있는 모든 값과 그 가능성을 보여주기 때문에 아래와 같은 경우 필요함.
- 전체적인 특성 파악 (확률 변수가 가질 수 있는 모든 경우에 대한 가능성을 알고 싶을 때)
- 예시: 동전 2번 던지기 실험에서 '앞면 횟수'(X)에 대한 평균(기댓값)이나 분산을 계산하려면 P(X=0), P(X=1), P(X=2) 모두 필요.
- 복잡한 확률 계산 (특정 범위에 대한 확률을 계산하거나 여러 사건을 조합해야 할 때)
- 예시: '앞면이 1회 이상 나올 확률'이 궁금하다면, P(X=1) + P(X=2)를 합산해야 하므로 분포의 일부를 알아야 함.
- 통계적 모델링 (실제 데이터를 분석하고 미래를 예측하기 위해 '모집단의 형태(분포)'를 규정해야 할 때. 예를 들어 정규 분포, 이항 분포 등 특정 모델을 가정할 때)
1) 이산형 확률 분포 (discrete probability distribution)
- 이산형 확률변수 X가 특정 값을 가질지에 대한 확률을 나타내는 분포 형태 ⇒ 이산형 확률분포
- 베르누이분포, 이항분포, 기하분포, 포아송 분포 등이 있다.
- 예를 들어 주사위를 한번 던졌을 때 6이 나오는 횟수인 확률변수(X)는 0, 1 값을 가질 수 있다. 값의 범위가 유한이고 셀 수 있으므로, 이는 이산형 확률변수의 확률분포를 따른다고 할 수 있다.
▶ 확률질량함수 (probability mass function)
- 이산 확률변수의 확률분포는 확률질량함수를 이용하여 표현한다.
- 즉, 확률질량함수란 이산 확률변수가 특정 값을 가질 확률을 나타내는 함수


▶ 누적분포함수 (cumulative distribution function)
- 확률질량함수 성질 ③의 특수한 형태
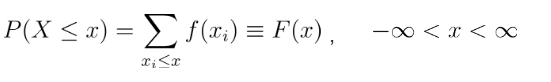





2) 연속형 확률 분포 (continuous probability distribution)
- 연속형 확률변수 X가 특정 구간에 포함될지에 대한 확률을 나타내는 분포 형태 ⇒ 연속형 확률분포
- 정규분포, 지수분포, 균일분포, 카이제곱분포, F분포 등이 있다.
- 예를 들어 대한민국에 거주하는 20살 남자의 키라는 확률변수(X)가 취할 수 있는 값들은 특정 값이 아닌 특정 실수 구간에 포함될 것이기 때문에 셀 수 없으므로, 이는 연속형 확률변수의 확률분포로 표현할 수 있을 것이다.
▶ 확률밀도함수 (probability density function)
- 연속 확률변수의 확률분포는 확률밀도함수를 이용하여 표현한다.
- 즉 확률밀도함수란 연속 확률변수가 특정 구간에 포함될 확률을 나타내는 함수
- 연속형 확률변수는 취할 수 있는 값이 셀 수 없는 무한대이기 때문에, 확률밀도함수가 가능한 값 하나하나에 확률을 부여하지 않고, 구간에 확률을 부여하게 된다. 그러므로 연속형 확률변수에서 확률은 항상 면적으로 표시되고, 연속형 확률 변수에서 어떤 한 값에 대한 확률은 0이다.

• 히스토그램의 면적 ⇒ 해당 구간에서의 비율(상대도수)
• 확률밀도함수의 면적 ⇒ 해당 구간에서의 확률(그 구간에 상대적으로 얼마나 밀집되어 있는지 나타낸 것)


▶ 누적분포함수
- 확률밀도함수 성질 ③의 특수한 형태





[참고자료]
Future accountant / Trial, Experiment, Event, Result/Outcome - Probability
https://www.futureaccountant.com/probability/study-notes/trial-result-event-outcome.php#.YvmljHZBxD8
장철원님 블로그 확률변수
장철원님 블로그 확률분포
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 확률변수의 분산과 표준편차 (0) | 2022.08.18 |
|---|---|
| 기초통계 / 확률변수의 기대값 (0) | 2022.08.18 |
| 기초통계 / 표본 공분산, 표본 상관계수 (0) | 2022.08.15 |
| 기초통계 / 자료를 파악하는 방법 (표, 그래프) (0) | 2022.08.15 |
| 기초통계 / 분포 형태를 나타내는 측도 (왜도, 첨도) (0) | 2022.08.14 |