[참고] 추론 방식의 구분
1. 논리적 추론
- 연역적 추론: 일반적/보편적 전제로부터 개별적/특수한 결론을 얻는 추론 방식
- 귀납적 추론: 개개의 특수한 사실로부터 일반적인 결론을 이끌어내는 추론 방식
2. 통계적 추론
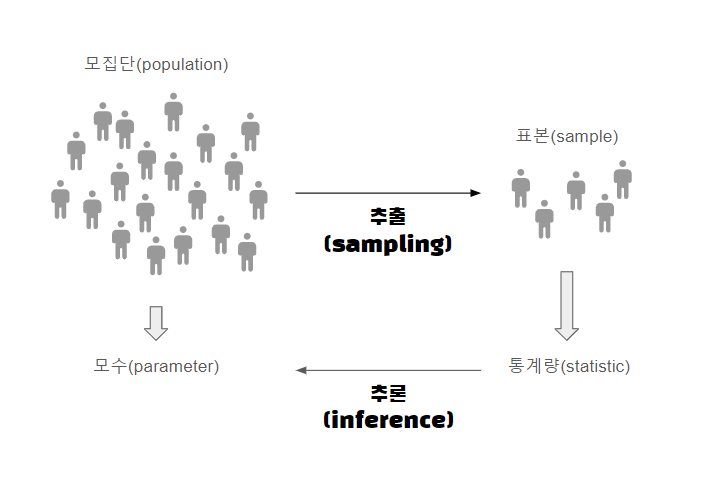
통계적 추론 (Statistical Inference)
표본 정보를 이용하여 미지의 모수 값을 도출해내는 과정
통계적 추론의 분류
1. '모집단에 대한 분포 가정 여부' 에 따라
(1) 모수적 추론 (parametric inference)
- 모집단에 특정 분포를 가정하고 모수에 대해서 추론하는 것.
- 모집단에 대한 가정이 얼마나 적절한지에 따라 최종 결론의 타당성에 영향을 주기 때문에 ⇒ 가정의 적절성을 평가하는 부분이 포함됨 (예를 들어 정규성 검정)
- 자료가 정규분포, 등간척도, 비율척도인 경우
(2) 비모수적 추론 (non-parametric inference)
- 모집단에 대해 특정 분포 가정을 하지 않음.
- 모집단에 대한 특정 분포 가정을 하지 않기 때문에, 모집단의 특성을 몇 개의 모수로 결정하기 어려움. 그래서 수많은 모수가 필요할 수 있음.
- 어떤 특정한 모수에 관심이 있지 않으므로 나름대로 직관적인 방법으로 추론하는 경향이 있다. 따라서 다양한 형태의 통계량들을 고려할 수 있고, 이들 통계량의 성질을 유도하고 이를 기반으로 하여 통계적 추론을 진행한다. ⇒ 그러나 모수적 추론에 비해 유도과정이 어려운 경우가 많음.
- 모수 자체보다 분포 형태에 관한 검정을 실시함.
- 표본수가 적고, 명목척도, 서열척도인 경우 또는 극단적인 이상치가 있는 경우
- 대표적인 방법으로 자료의 순위를 사용함.
2. '추론 목적' 에 따라
(1) 추정
: 표본의 통계량(평균, 분산 표준편차)을 사용하여 모집단의 모수를 구체적으로 추측하여 결정하는 것.
- 점추정: 하나의 값으로 모수의 값이 얼마인지 추측함.
- 구간추정: 모수를 포함할 것으로 기대되는 구간을 확률적으로 구함.
(2) 가설검정
모수에 대한 가설을 세우고 그 가설의 옳고 그름을 확률적으로 판정하는 방법론
3. '모수처리 방식' 에 따라
(1) 빈도론자 추론 (frequentist inference)
- 확률을 사건의 빈도로 보는 관점. 확률은 장기적으로 일어나는 사건의 빈도라고 주장함.
- 특정한 사건이 얼마나 반복되어 발생하는지 관찰하고 가설을 세워 모델을 만들어서 검증하는 것.
- 모수(=우리가 알아내고자 하는 값)는 고정되어 있는 값 '상수'
-
(2) 베이지안 추론 (bayesian inference)
- 확률을 사건 발생에 대한 믿음 또는 척도로 바라보는 관점
- 모수(=우리가 알아내고자 하는 값)는 확률적으로 변하는 값 '확률 변수' ⇒ 그래서 모수의 확률 분포가 무엇인지에 대해 관심을 가
⭐(1)과 (2)는 확률을 해석하는 관점의 차이라고 할 수 있음.
[참고 자료]
http://www.ktword.co.kr/test/view/view.php?m_temp1=1784
통계적 추론
Inferential Statistics, Inductive Statistics, 추정 통계학, 추리 통계학, 추측 통계학, 추론 통계학, 추론 통계, 추정 검정
www.ktword.co.kr
https://shawnbaek.tistory.com/14
[Baysian 1] 빈도주의(Frequentist) VS 베이지안(Baysian)
보통 통계학에서 한 사건이 장기적으로 일어날 때 발생하는 빈도를 확률이라고 한다. 확률을 사건의 빈도로 보는 것을 빈도주의(frequentist)라고 하고 확률을 사건 발생에 대한 믿음 또는 척도로
shawnbaek.tistory.com
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 표본 추출 시, 가중치 조정이란? (0) | 2024.02.14 |
|---|---|
| 기초통계 / 이산형 확률분포 (1) 베르누이 분포, 이항 분포 (0) | 2022.08.18 |
| 기초통계 / 확률변수의 분산과 표준편차 (0) | 2022.08.18 |
| 기초통계 / 확률변수의 기대값 (0) | 2022.08.18 |
| 기초통계 / 확률 변수, 확률 분포 (0) | 2022.08.16 |