기초통계 / 분포 형태를 나타내는 측도 (왜도, 첨도)

💡자료의 분포 형태를 알아야 하는 이유

• 어떤 통계분석 방법을 선택할 지는 '자료의 속성/형태' 와 '분석 목적' 에 따라 달라진다.
• 즉, 분석하고자 하는 자료가 통계분석 방법에서 가정한 조건을 얼마나 만족하는지에 따라 분석 방법의 적절성이 결정된다.
• 특히 많은 통계분석 방법에서 모집단의 분포가 중심위치를 기준으로 대칭(symmetric)한다고 가정한다.
• 따라서 자료가 모집단의 가정을 만족하는지 확인하기 위해서는, 자료의 분포 형태에 대한 측도를 확인할 필요가 있는 것이다.

 

 

왜도(skewness)

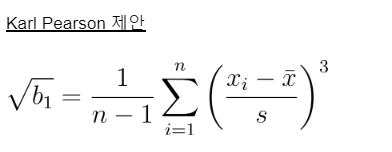
• 자료의 분포가 대칭적인지 or 한쪽으로 치우쳐있는지를 나타내는 측도

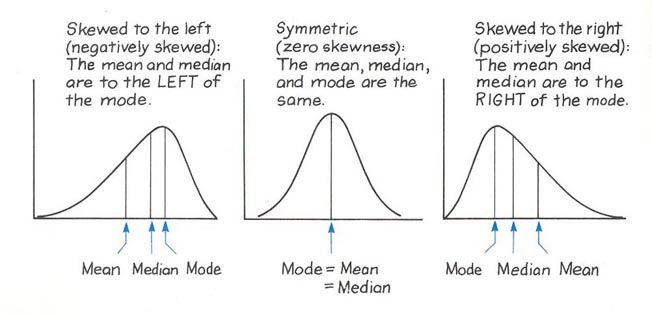
• 큰 음수: 왼쪽으로 꼬리가 긴 분포

• 큰 양수: 오른쪽으로 꼬리가 긴 분포

• 0 에 가까울수록 대칭을 이루는 분포

 

출처 - http://webbuild1.knu.ac.kr/~bskim/normality.htm

 

 

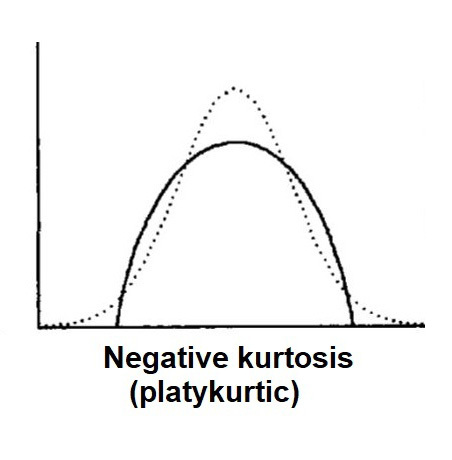
첨도(kurtosis)

• 양쪽 꼬리가 얼마나 두터운지를 나타내는 측도

• 분포의 중심보다는 꼬리부분이 얼마나 두터운지에 따라 영향을 많이 받기 때문이다.

• 첨도가 클수록 이상치가 많을 수 있다. (왜냐하면 꼬리가 얇고 긴 형태를 띠기때문에)

• 경우에 따라 위의 식에서 3을 빼주는 형태로 많이 사용하는데, 그 이유는 정규분포에 가까운지 확인하는데 사용하기 위하해서다. (정규분포의 경우 이론적으로 첨도가 3이기때문에)

 

출처 - https://www.simplypsychology.org/kurtosis.html

 

 

 

왜도와 첨도의 활용

• 이상치 확인: 왜도나 첨도의 값이 심하게 큰 경우, 자료에 이상치가 있을 가능성이 높다. 

• 정규성 검정: 정규분포의 왜도=0, 첨도=3 이므로, 이를 활용하여 정규성을 검정할 수 있다. (Jacque-Bera test)

 

 

 

[참고자료]

경북대학교 - 왜도, 첨도, 정규성

http://webbuild1.knu.ac.kr/~bskim/normality.htm

 

갈릭님 블로그 - 왜도 첨도

https://blog.naver.com/yk60park/222100758577