표본 크기


대표값
- 자료의 중심을 나타내는 값으로서 자료 전체를 대표할 수 있는 값.
- 적절한 대표값을 찾고 확인하는 이유는 자료의 분포를 전체적인 맥락에서 중심 경향성에 대해 살펴보기 위함이다.
- 같은 의미로 중심 경향치, 집중화 경향성, 중심위치의 측도라는 용어를 사용하기도 한다.
- 가장 많이 사용되는 대표값은 평균이다.
표본평균(sample mean)

• 자료 전체의 무게중심을 의미한다.
• 표본평균은 표본의 모든 값을 더하여 표본 크기로 나누어 구한다.
• 표본평균은 '관측값 x 상대도수'의 합계로도 나타낼 수 있다. ★

예시
어느 고등학교 학생의 키를 조사하기 위해 5명을 표본으로 뽑았다고 하자.
- 표본: 162, 157, 170, 177, 168
- 표본 크기: 5
- 표본 평균은 두 개의 방법으로 표현할 수 있다.
① (162 + 157 + 170 + 170 + 177 + 168) / 6 = 167.3 ⇦ 관측값 합계 / 표본 크기
② 162x1/6 + 157x1/6 + 170x2/6 + 177x1/6 + 168x1/6 = 167.3 ⇦ '관측값 x 상대도수'의 합계
1) 평균의 종류
• 산술평균: 일상에서 평균은 '산술평균' 을 의미한다.
• 가중평균(weighted mean)
• 기하평균(geometric mean)
• 조화평균(harmonic mean)
2) 평균의 함정
평균은 자료 전체의 합을 계산에 사용하기 때문에, 자료의 이상치 포함 여부에 따라 평균값에 차이가 크게 나는 경향이 있다. 즉 평균은 이상치에 영향을 많이 받는다. 이를 '평균은 이상치에 강건성(Robust, Roubustness)이 없다' 또는 '평균은 이상치에 로버스트하지 않다' 라고도 한다. 이렇게 자료에 이상치가 포함되어 평균이 대표성을 갖는다고 보기 어려운 경우 대표값을 평균이 아닌 중앙값, 절사평균, 최빈값 등 다른 통계값으로 대체하는 것을 고려할 수 있다.
따라서 우리는 자료의 전체적인 산포도를 항상 함께 살펴보고, 동시에 중앙값이나 최빈값도 확인하면서 평균의 함정에 빠지지 않도록 주의해야한다.
💡 강건성(Robust, Robustness) 이란?
- 로버스트하다는 것은 이상치에 민감하지 않은 경향을 말함
- 이상치(Outlier) : 전체 자료 중 대부분의 값들로부터 멀리 동떨어져있는 값들을 말함
3) 표본비율도 일종의 표본평균이다.
💡표본비율(sample proportion) 이란?
- 모집단에서 어떤 특성을 갖는 사건에 대한 비율을 그 사건에 대한 모비율이라고 한다.
- 표본에서 어떤 특성을 갖는 사건에 대한 비율을 그 사건에 대한 표본비율이라고 한다.
- 어떤 특성을 갖는 사건 A가 일어난 횟수를 n(A)라고 하면, 그 사건에 대한 표본비율은 ⇒ n(A)/n
⇒ 예를 들어 표본 크기가 n인 표본이 있다. x_i(= i번째 관측값)이 관심 범주에 속하면 x_i의 값을 1로, 속하지않으면 0으로 표시하기로 하자. 그러면 모든 관측값을 다 합했을 때 해당 관심 범주에 포함된 표본의 수가 계산된다. x_1 + x_2 + ... + x_n = Y 그렇다면 여기서 표본비율을 Y/n 라고 나타낼 수 있고 이는 표본평균과 의미가 같음을 알 수 있다.
중앙값(median)
• 자료를 크기순으로 나열했을 때 제일 가운데에 위치하는 값
• 아래 또는 위로 세어봐도 같은 중앙 위치
• 중간값 = 중위수 = 50 백분위수 = 2 사분위수
1) 중앙값 계산 방법
🔽 n이 홀수일 때
• 중앙에 위치한 하나의 값을 취함
• (n+1)/2 번째에 위치한 하나의 값을 취한다.
예시
| 데이터 | 1, 3, 5, 7, 9 |
| 데이터 개수(n) | 5 ⇒ 홀수 |
| 중앙값 계산과정 | (n+1)/2 = 3번째 값 ⇒ 5 |
| 중앙값 | 5 |
🔽 n이 짝수일 때
• 중앙에 위치한 두 값의 평균을 취함
• (n/2) 번째 값과 (n/2)+1 번째 값의 평균을 취한다
예시
| 데이터 | 1, 3, 7, 9 |
| 데이터 개수(n) | 4 ⇒ 짝수 |
| 중앙값 계산과정 | (n/2) = 2번째 값과 (n/2)+1 = 3번째 값의 평균 ⇒ (3 + 7) / 2 = 5 |
| 중앙값 | 5 |
예시
| 데이터 | 2, 1, 4, 6, 5, 6, 7, 9 |
| 데이터 정렬 | 1, 2, 4, 5, 6, 6, 7, 9 |
| 데이터 개수(n) | 8 ⇒ 짝수 |
| 중앙값 계산과정 | (n/2) = 4번째 값과 (n/2)+1 = 5번째 값의 평균 ⇒ (5 + 6) / 2 = 5.5 |
| 중앙값 | 5.5 |
2) 중앙값 특징
단점
평균은 자료의 모든 값을 더하여 구하기 때문에 모든 값을 사용하지만, 중앙값은 모든 값을 크기 순으로 나열한 뒤 가운데를 찾아 그 값만 사용한다. 즉 자료의 정보를 다 활용하지 못한다는 단점이 있다.
장점
평균은 자료의 모든 값을 더하여 구하기 때문에 이상치에 영향을 받지만, 중앙값은 모든 값을 크기 순으로 나열한 뒤 가운데를 찾는 것이므로 이상치에 크게 영향을 받지 않는다. 중앙값은 이상치에 강건성(Robust, Roubustness)이 있다. (= 중앙값은 이상치에 로버스트하다)
✔️ 평균과 중앙값이 비슷하다면 ⇒ 모든 자료의 정보를 활용하는 '평균'을 대표값으로 사용할 것을 제안!
✔️ 평균과 중앙값이 차이난다면 ⇒ 대표값으로 '평균' or '중앙값' 선택? 그건 고민해봐야할 문제. 자료의 형태에 따라 혹은 분석 목적에 따라 적절히 선택할 필요가 있다.
[예시1]
• 자료의 분포가 한쪽 꼬리로 치우쳐서 비대칭적일 때
-> 소득의 분포는 오른쪽으로 꼬리가 긴 대표적인 비대칭 분포이고, 고소득층과 저소득층의 소득 격차가 워낙 크기때문에 산술 평균을 내면 고소득층의 소득 비중이 높아져버린다. 그래서 이런 경우 산술 평균은 대표값으로서 의미가 없으므로 모든 국민을 소득 순으로 줄세우기를 한 다음, 중앙에 있는 50백분위수(중앙값)를 국민 가구소득의 기준으로 삼는다. 기준 중위 소득이라고 함.
[예시2]
• 자료에 극단적인 이상치가 있을 때
-> 직원이 총 100명인 회사에서 99명의 일반 직원들의 평균 연봉은 4000만원인데 사장의 연봉만 50억인 경우, 사장을 포함한 회사의 평균 연봉은 8960만원이 되버리기 때문에 '평균'은 대표성을 갖는다고 보기 어렵다. 따라서 이와 같은 경우 평균보다 중앙값이 유용하게 사용된다. -> 평균값: 8960만원😵, 중앙값: 4000만원🙂
[예시3]
• 자료를 수집하는 중인데, 극단의 관찰값이 확정되지 않았을 때
• 자료를 수집하는 중인데, 자료가 극단성을 포함할 여지가 있도록 개방된(open-ended) 경우
-> 학생이 총 30명인 A반 전체 학생들의 퍼즐을 푸는 평균 시간을 측정하려고 한다. 29명은 10분 언저리에서 풀었지만 1명은 측정 한계시간 1시간을 넘기도록 여전히 못풀어서 측정이 중단 되었다. 이미 평균은 의미가 없어졌기 때문에 중앙값을 이용해야 한다.
절사평균(trimmed mean)
• 평균은 모든 자료의 정보를 사용하지만, 이상치에 로버스트하지 않음
• 중앙값은 이상치에 로버스트하지만, 모든 자료의 정보를 다 활용하지 못함
• 그래서 이를 보완하기 위해 α % 절사평균을 사용하기도 한다. 중앙값을 계산하는 것처럼 순서통계량으로 정렬한 뒤 하위 α % 부터 상위 α %까지의 자료를 이용하여 표본평균을 계산하는 것이다.
• α 를 적절하게 정하면 이상치에 로버스트하면서도 자료의 정보를 많이 활용할 수 있게 된다.
• 간단하게 n개의 자료중 순서통계량 위아래로 k개씩을 제외한 나머지 n-2k개의 표본평균을 구하여 나타내기도 한다.
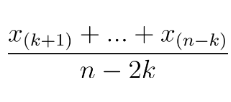
• 체조나 피겨스케이팅 등에서 채점할 때 절사평균을 활용한다.
최빈값(mode)
• 가장 빈번하게 등장하는 값
• 최빈값은 여러 개가 나올 수 있다.
• 이산형 자료에서 주로 사용된다.
• 연속형 자료의 경우 없을 수도 있다.
분포 모양에 따른 대표값 위치
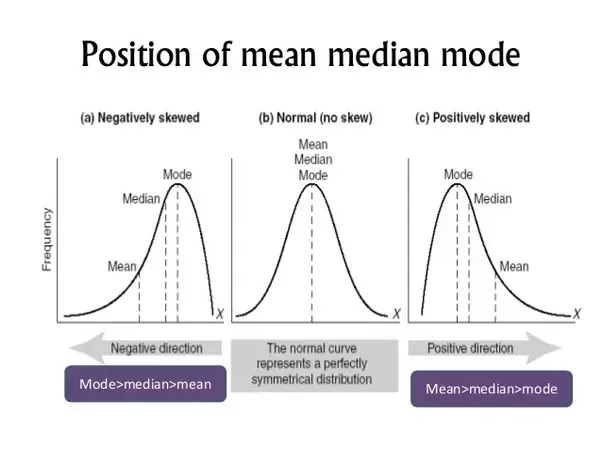
요약
자료의 종류, 산포도 등 데이터의 성격에 따라 대표성을 잘 나타내는 대표값은 달라질 수 있다. 따라서 데이터를 세밀하게 살펴보고 해당 데이터를 가장 잘 나타낼 수 있는 대표값을 선택해야할 것이다. 특히 주로 사용되는 대표값인 평균만 무조건적으로 보지 않고 자료의 산포와 중앙값이나 최빈값과 같은 다른 대표값들도 함께 보며 자료를 제대로 파악하는 것이 중요하다.
[참고자료]
나무위키 - 대푯값 (https://namu.wiki/w/%EB%8C%80%ED%91%AF%EA%B0%92)
정보통신기술용어해설 - 중위수, 중앙치, 중앙값 (http://www.ktword.co.kr/test/view/view.php?m_temp1=1637)
뷰저블 - 데이터 분석을 위한 기본 통계, 대표값과 평균의 종류 (https://www.beusable.net/blog/?p=3855)
블로그 세상은 아름답다 - 중간값/중앙값 (https://theworldisbeautiful.tistory.com/304)
블로그 빅데이터, 인공지능, 프로... - 평균, 중앙값, 최빈값 (https://lsh-story.tistory.com/76)
DBR - 강 평균 깊이 150cm, 우리 군사들 건너라? '평균의 함정'에 빠지면 목숨도 위험하다 (https://dbr.donga.com/article/view/1303/article_no/6962/ac/magazine)
블로그 척도와 집중경향성, 그 기본 성질에 대한 총 정리(https://opinion.krsocsci.org/209)
블로그 데잇걸즈2
https://dataitgirls2.github.io/tutorial/Tutorial_180629_Statistics.html
오빠두엑셀 - 엑셀 기하평균, 언제 어떻게 사용하는 걸까?
https://www.oppadu.com/%EC%97%91%EC%85%80-%EA%B8%B0%ED%95%98%ED%8F%89%EA%B7%A0/
블로그 잇찌 - 산술평균 기하평균 조화평균 생활 속 예시
https://blog.naver.com/ink2777/222497565094
블로그 BallPen.blog - 평균 – 산술, 기하, 조화 평균의 개념과 실생활 활용
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 자료를 파악하는 방법 (표, 그래프) (0) | 2022.08.15 |
|---|---|
| 기초통계 / 분포 형태를 나타내는 측도 (왜도, 첨도) (0) | 2022.08.14 |
| 기초통계 / 산포도 (사분위범위, 표본 분산, 표본 표준편차, 변동계수) (0) | 2022.08.14 |
| 기초통계 / 자료의 종류, 척도의 종류 (0) | 2022.07.07 |
| 기초통계 / 모집단과 표본 (0) | 2022.07.07 |