💡자료의 속성을 알아야 하는 이유
• 어떤 통계분석 방법을 선택할 지는 '자료의 속성/형태' 와 '분석 목적' 에 따라 달라진다.
• 즉, 분석하고자 하는 자료가 통계분석 방법에서 가정한 조건을 얼마나 만족하는지에 따라 분석 방법의 적절성이 결정된다.
• 그러므로 자료를 속성에 따라 분류하여 공부할 필요가 있는 것이다.
자료(data)

변수
조사 대상에 따라 다른 값으로 나타날 수 있는 특성 혹은 속성
일변량 자료(univariate data): 하나의 변수만 있는 자료
다변량 자료(multivariate data): 여러 개의 변수들이 있는 자료. 변수들 간 관련성은 있을 수도 있고, 없을 수도 있다.
관측 개체
관측치, 관측값이라고도 한다. 관측 개체들 간 관련성이 있을 수도 있고, 없을 수도 있. 단, 기초 통계에서는 관측 개체들 간 관련성이 없고 각각 독립된 개체라고 기본적으로 가정한다.
자료의 형태/특성에 따른 분류
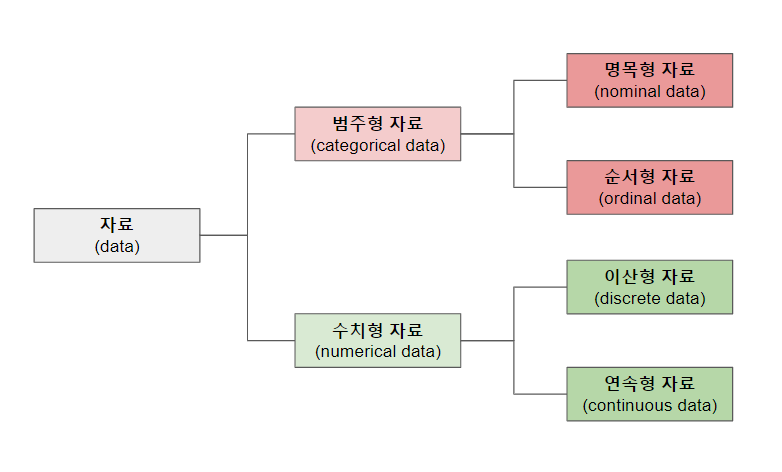
1. 범주형 자료(categorical data)
질적자료(qualitative data)를 보통 범주형 자료로 나타낸다.
1-1. 명목형 자료(nominal data)
• 숫자로 바꿔도 그 값이 크고 작음을 나타내지 않고, 단순히 범주를 의미함.
• 혈액형 A, B, O, AB 를 숫자 1,2,3,4 로 바꿔도 되지만, 그 숫자가 크고 작음을 의미하는 것이 아니다. AB를 4로 표시한 것 뿐이지 AB가 4니까 제일 크다라고 말하는 건 이상하다.
1-2. 순서형 자료(ordinal data)
• 범주의 순서로 상대 비교 가능함.
• 수치형 자료를 범주화하여 순서형 자료로 바꾼 경우도 있다.
• 비만도는 수치형 자료(몸무게, 키)들을 이용하여 계산한 값을 범주화한 순서형 자료이다.
• 비만도(저체중, 정상, 과체중, 비만, 고도비만), 만족도(불만족, 보통, 만족)
< 범주형 자료(categorical data) 정리 방법 >
일변량 자료라고 가정한다.
(1) 도수분포표
• 각 범주에 몇 개의 관측 개체가 있는지 '도수분포표'로 정리한다.
• 도수(frequency): 범주의 속한 관측 개체의 수 (=빈도)
• 상대도수(relative frequency): 전체 자료 중 해당 범주에 속한 자료의 비율
• 순서형 자료의 경우 '누적'도수 및 '누적'상대도수를 같이 정리하면 자료를 파악하는데 도움이 된다.
(2) 원 도표 (pie chart)
• 상대도수를 파이차트로 표현할 수 있다.
• 원을 사용하는 이유는 다른 도형과 달리 각도와 면적의 비율이 항상 동일하기 때문이다.
• 단 파이차트는 '비교'에 부적합할 수 있다. 특히 비슷한 비율의 범주들이 존재하거나 범주가 너무 많은 경우 비교하기 매우 어렵다.
(3) 막대 그래프 (bar chart)
• 각 범주의 도수나 상대도수를 막대 길이로 표시하여 나타낸다.
• 차이에 대한 인지 순서 by Cleveland(1985)
- 동일한 척도에서의 위치 → 길이 → 각도&기울기 → 면적 → 부피 → 색상&밀도
• 즉 비교를 할 때는 파이 차트보다 막대 그래프가 더 적합하다고 할 수 있다.
2. 수치형 자료(numerical data)
양적 자료(quantitative data)를 보통 수치형 자료로 나타낸다.
2-1. 이산형 자료(discrete data)
• 셀 수 있음. (countable data)
• 범주형 자료의 발생 빈도를 나타내어 수치형 자료로 나타낼 수 있다.
• 충치 수는 충치 여부(있다/없다)의 발생 빈도를 나타낸 수치형 자료이다.
• 어금니1: 충치 있다 / 어금니2: 충치 없다 / 앞니1: 충치 없다 / 그 외 나머지 : 충치 없다. => 충치 수: 2
2-2. 연속형 자료(continuous data)
• 연속적이라 셀 수 없음.
• 연속형 자료는 대부분 이산화를 통해 절사된 형태로 표시한다.
• 키를 171cm 정수형태로 보통 표시하지만, 정확히는 170.5~171.5cm 사이 어딘가 171.0124... 일 것.
• 즉 키는 정확하게 나타낼 수 없는, 셀 수 없는 숫자이기때문에 연속형 자료라고 할 수 있다.
< 수치형 자료(categorical data) 정리 방법 >
일변량 자료라고 가정한다.
(1) 도수분포표
• 수치형 자료의 값이 몇 개로 한정된 경우에는 값 자체를 범주로 바로 사용해도 되지만,
• 대부분 그렇지 않기 때문에 자료를 '범주화'하여(그룹으로 묶어서) 순서형 자료 형태로 변환한 뒤, 도수분포표를 작성한다. 순서형 자료를 도수분포표로 나타낼 때는 도수, 상대도수, 누적도수, 누적상대도수를 표시할 수 있다.
💡범주화하는 방법
• 계급(class)의 수 결정 ➡️ 제곱근 방법, Sturges 공식, Rice 공식 등
• 계급 경계값 결정 ➡️ 기본적으로 동일 간격
- 방법들은 참조할 뿐, 분석하는 사람이 자료의 특성/구조를 고려하여 적절하게 결정하는 것이 중요하다.
- 예를 들어 '키'에 대한 자료가 있는데 최소값은 142cm, 최대값은 209cm라고 한다. 이때 분석하는 사람이 "최소점은 140cm, 최대점은 210cm로 하고 기본 계급구간은 10cm로 하되 도수가 적은 계급구간은 통합하자" 라고 정할 수 있는 것이다. 이렇게 해서 데이터의 특성을 파악하는데 도움이 된다면 문제가 없다.
(2) 점 도표 (dot plot)
• 각 관측값의 위치에 점을 표시하고 같은 관측값이 있는 경우 위로 누적한다.
(3) 히스토그램 (histogram)
• 히스토그램은 수치형 자료 특히 연속형 자료의 분포 형태를 표시한다.
💡히스토그램 vs. 막대 그래프 차이는?
히스토그램
• 계급의 상대도수를 사각형의 면적으로 표시한다. (전체 면적의 합은 '1')
• 따라서 높이는 면적(상대도수)을 가로 길이(계급구간의 길이)로 나눈 값으로 표시한다. 통계학에서는 히스토그램의 높이를 '밀도(density)'라고 말한다.
막대그래프
• 계급의 상대도수나 도수를 막대의 높이로 표시한다.
즉 계급 구간이 모두 동일한 간격이면 히스토그램이나 막대 그래프의 형태가 같게 나타나겠지만, 동일하지 않은 간격의 구간이 포함되어 있다면 형태가 다르게 나타날 것이다.
(4) 줄기-잎 그림(stem-and-leaf plot)
• 관측값의 정보를 그대로 간직하면서 자료의 분포를 알려주는 그림
• 히스토그램은 자료의 분포를 알려주지만 개별 관측값의 정보는 알 수가 없음.
(5) 상자그림(box plot)
• 수치 자료 분의 산포를 알려주는 그림.
3. 정리
• 범주형 자료의 발생 빈도를 '수치형 자료'로 나타낼 수 있다.
• 수치형 자료를 범주화하면 '순서형 자료'로 나타낼 수 있다.
• 즉 자료들을 하나의 고정된 형태로만 생각하지 말자. 왜냐하면 위 처럼 형태를 바꿔서 표현할 수 있기 때문이다. 상황에 따라 적절히 변환해서 사용할 수 있는 것이다. 그러니 서로 별개로 떼어놓고 생각하지 말고 연결고리를 만들어 생각하자.
• 단, 여기서 중요한 점은 자료의 형태를 바꿔서 표현할 때 기존 정보의 손실이 발생할 수 있으니 반드시 유의하자.
척도
1. 척도란?
• 사람이나 사물 등 관측 대상의 특성을 수량화하기위해서 단위나 규칙을 가지고 숫자를 부여한 것.
• 즉 질적자료를 양적자료로 변환시키는데 사용하는 도구
2. 척도의 분류
범주형 척도
(1) 명목척도(명명척도), nominal scale
• 단순하게 측정 대상의 특성을 분류하거나 확인하기 위함
• 숫자로 바꿔도 그 값이 크고 작음을 나타내지 않고 범주를 표시함
• 예) 성별, 혈액형, 출생지역 등
(2) 서열척도(순위척도), ordinal scale
• 항목들 간 서열이나 순위가 존재
• 크고 작음 or 높고 낮다 등의 순위만 제공할 뿐 양적인 비교는 할 수 없음
• 예) 성적(A, B, C, D, F), 선호도, 만족도(Likert 척도) 등
연속형 척도
(1) 등간척도(구간척도), interval scale
• 절대 0점은 존재하지 않으며, 대상이 갖는 양적인 정도의 차이에 따라 등간격으로 숫자를 부여한 척도
• 순위 사이의 간격이 동일하여 양적인 비교가 가능함.
• 예) 온도계, 물가지수 등
(2) 비율척도, ratio scale
• 절대 0점이 존재하여 비율계산이 가능한 숫자를 부여한 척도
• 예) 몸무게, 나이, 형제의 수, 직장까지의 거리 등
자료의 성격에 따른 통계분석 기법 선택
1. 범주형(종속변수) + 범주형 변수(독립변수)
교차분석(카이제곱검증)
2. 범주형(종속변수) + 연속형 변수(독립변수)
판별분석, 군집분석, 로지스틱회귀분석
3. 연속형(종속변수) + 범주형 변수(독립변수)
t-검증, 분산분석, 다변량분산분석
4. 연속형(종속변수) + 연속형 변수(독립변수)
상관분석, 회귀분석, 경로분석/구조방정식모델링분석
[참고자료]
블로그 - 통계 자료의 종류
(https://m.blog.naver.com/bloomingds/221232161942)
블로그 - 통계의 시작 - 자료와 변수의 종류
(https://drhongdatanote.tistory.com/3)
블로그 - 통계의 시작 - 척도의 종류
(https://drhongdatanote.tistory.com/8)
블로그 - 척도(Scale)
(https://m.blog.naver.com/firerisk/220865466294)
블로그 - 척도의 종류와 의미
(https://m.blog.naver.com/moses3650/221202517582)
블로그 - 척도와 집중경향성, 그 기본 성질에 대한 총 정리
(https://opinion.krsocsci.org/209)
블로그 - RPubs / ch5 측정척도의 유형과 내용 (통계기법의 선택)
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 자료를 파악하는 방법 (표, 그래프) (0) | 2022.08.15 |
|---|---|
| 기초통계 / 분포 형태를 나타내는 측도 (왜도, 첨도) (0) | 2022.08.14 |
| 기초통계 / 산포도 (사분위범위, 표본 분산, 표본 표준편차, 변동계수) (0) | 2022.08.14 |
| 기초통계 / 대표값 (평균, 중앙값, 절사평균, 최빈값) (0) | 2022.08.12 |
| 기초통계 / 모집단과 표본 (0) | 2022.07.07 |