산포도
• 자료들이 얼마나 퍼져 있는지를 나타내는 측도
• 중심위치(대표값)가 얼마나 안정적인지에 대한 중요한 정보를 제공
- 자료가 조밀하게 모여있다. ⇒ 중심위치의 변동이 작아짐
- 자료가 넓게 퍼져있다. ⇒ 중심위치의 변동이 커짐
• 범위, 사분위 범위, 분산, 표준편차, 절대편차, 변동 계수 등
범위
• 자료 중 가장 큰 값과 작은 값의 차이
• 최대값과 최소값에만 영향을 받기때문에 자료 전체에 대해 퍼져있는 정도를 파악할 수는 없다. 그래서 실제 산포도로서 많이 사용되지는 않는다.
사분위 범위
1) 사분위수(quartile)
자료를 오름차순으로 정렬한 뒤, 동일한 비율로 4등분할 때의 세 위치
• 25%지점 → 제 1사분위수
• 50%지점 → 제 2사분위수 = 표본중앙값
• 75%지점 → 제 3사분위수
2) 사분위 범위(IQR)
제 3사분위수와 제 1사분위수의 차이
3) 사분위수 계산 방법

🔽 k가 정수인 경우: 순서통계량 k번째 수가 해당 사분위수

🔽 k가 정수가 아닌 경우: 비례에 의한 내삽법을 적용



4) 상자그림(box plot)
자료의 주요 위치 파악과 이상치 검출 등에 사용된다.


[참고] IQR 방식에서 IQR의 계수로 1.5를 사용하는 이유
https://djccnt15.github.io/dataanalysis/iqr_method/
편차(deviation)

• 자료의 변량에서 평균을 뺀 값.
• 편차의 총합은 항상 0.
• 편차의 절대값이 클수록 변량들이 평균에서 멀리 떨어져 있고,
• 편차의 절대값이 작을수록 변량들이 평균에 가까이 붙어 있다.
모든 자료들 간의 거리의 합을 이용해보자!
1) 먼저 두 점의 거리를 나타내는 두 가지 방법이 있다.

2) 그렇다면 모든 자료들 간의 거리의 합도 두 가지 방법으로 나타낼 수 있을 것이다.

• 자료들이 전체적으로 넓게 퍼져있으면 이 값은 커질 것이고 모여있으면 작아질 것이다.
• 다만 이렇게 모든 자료들 간의 거리의 합을 있는 그대로 구하면 결국 n 의 제곱만큼 더하기를 해야하므로 계산이 다소 번거로울 수 있다. 그래서 좀 더 효율적인 계산을 하기 위해 다른 방법이 고안되었다.
3) 중심위치 a와 모든 자료들 간 거리의 합으로 나타내보자.

여기서 적절한 중심위치 a는 어떻게 선택해야 할까?
• a와 자료들 간 거리의 합을 최소로 만드는 값이 적절한 a라고 할 수 있다.
• ②번부터 적절한 a 값을 확인해보자. ②번은 a에 대한 2차방정식의 합이다. 그러므로 간단하게 a에 대해 미분하여 0이 되는 값을 구하면 될 것이다. 그러면 결국 적절한 a는 표본 평균 값이 되는 것을 확인할 수 있다.
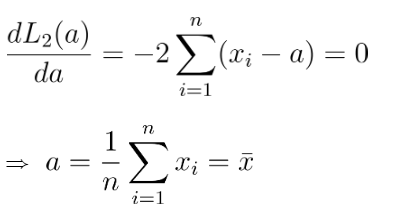
• ①번의 경우 a 로 미분불가능하지만, 그림을 그려보며 생각해보면 결국 적절한 a는 중앙값이 되는 것을 확인할 수 있다.

• 적절한 a 값을 확인했으니, 식을 다시 정리해보면 이렇게 쓸 수 있다. ①번 방법으로 퍼져있는 정도를 나타내고 싶다면 a를 중앙값으로 사용하고, ②번 방법으로 퍼져있는 정도를 나타내고 싶다면 a를 표본평균으로 사용해야한다. 여기서 ②번 방법을 정리한 식을 보면 결국 '편차의 제곱'의 합이 됨을 알 수 있다.(중요)

• ②번 방법을 보통 사용하는데 이 방법을 그대로 사용하여 퍼져있는 정도를 나타내는 것은 문제가 있다. 왜냐하면 계속 제곱을 해서 더하는 계산이므로 데이터가 많으면 많을수록 그 값의 크기가 계속 커질 것이기 때문이다. 즉 '데이터 개수가 많으면 많이 퍼져있다'라는 말은 못하게 표본의 크기를 보정해주어야 한다. 편차제곱을 표본의 크기로 나눠 평균을 냄으로써 표본의 크기를 보정해준 값이 바로 '표본 분산'이다.
표본 분산(sample variance)

• 편차를 이용하여 자료들이 평균을 중심으로 어느 정도로 흩어져있는지를 나타내는 값
• 편차제곱을 평균화하여 계산한다.
• 단, 편차 정보를 사용하기 때문에 n 이 아닌 n - 1 개의 편차 정보를 사용한다.
• 왜냐하면 편차의 총합은 0 이라는 제약조건때문에! ( n - 1 : 자유도 )
• 따라서 통계적 추론에서 표본 분산은 비편향추정량이 된다.
표본 표준편차(sample standard deviation)

• 표본 분산은 편차의 제곱합을 이용하므로 관측값 단위의 제곱이 되기때문에 숫자가 매우 커지게되고 단위도 바뀌어버리게된다. 그래서 표본 분산 값 자체는 산포를 직관적으로 이해하기 어려울 수 있다.
• 그렇기 때문에 눈으로 보는 산포와 일치하기 위해서는 자료를 측정할 때의 단위로 표시해야한다. 이를 위해 표본 분산에 루트를 씌운 값, 즉 표본 표준편차를 활용하여 표시한다.
표준편차의 이해

최근 10일동안 둘리와 또치는 둘다 하루 평균 8시간 공부했다고 한다. 평균 공부 시간이 같은 두 친구 중 누가 더 꾸준히 공부했다고 할 수 있을까? 평균 값이 같다고 두친구가 비슷하다고 말할 수 있을까? 이 때 표준편차를 계산하면 데이터를 다 확인하지 않아도 데이터의 분포를 어느 정도 파악할 수 있다.
<둘리>
평균: 8
표준편차: 5.3
평균 ± 표준편차: (2.7, 13.3)
⇒ 둘리는 가장 적게할 때는 대략 2.7시간, 가장 많이할 때는 13.3 시간 정도 했을 것으로 보이고
<또치>
평균: 8
표준편차: 1.6
평균 ± 표준편차: (6.4, 9.6)
⇒ 또치는 가장 적게할 때는 대략 6.4시간, 가장 많이할 때는 9.6 시간 정도 했을 것으로 보인다.
표준편차를 통해 데이터의 분포를 대략 유추해본 결과 둘다 하루 평균 8시간 공부했지만 또치가 표준편차가 더 작은걸로 보아, 둘리에 비해 또치가 더 꾸준히 공부했다고 말할 수 있을 것이다.
변동계수(coefficient of variation, cv)

• 위의 경우처럼 평균이 같은 표본들의 경우 표준편차만으로 산포를 비교할 수 있지만, 평균이 다른 표본들의 경우 표준편차만을 이용하여 산포를 비교하는 것은 적절하지 않을 수 있다.
• 평균이 다른 각 표본 사이의 표준편차를 비교할 때 평균의 영향을 없애주기 위해 표준편차를 산술평균으로 나누어줌으로써, 표준편차를 산술평균기준으로 표준화시킨 것을 '변동계수'라고 한다.
• 즉 변동계수는 자료의 상대적인 변동폭을 비교하는 측도가 된다.
• 변동계수의 값이 클수록 데이터 값의 차이가 상대적으로 크다는 것을 의미한다.

이번에는 평균 공부시간이 다른 둘리와 마이콜 둘 중에 누가 더 꾸준히 공부했는지 알아보려고 한다. 평균 값이 다르기때문에 평균 값의 영향을 없앨 수 있는 변동계수를 구하여 비교해보자. 둘리가 마이콜보다 표준편차의 절대적 값은 더 크지만, 변동계수 값 즉 상대적 변동폭은 더 작은 것으로 보아, 마이콜에 비해 둘리가 더 꾸준히 공부했다고 말할 수 있다.
표준화(standardization)

- 수능 시험은 과목별로 난이도가 다를 수 있기 때문에 원점수로 과목 간 성적을 비교하지 않는다. '표준화' 점수를 사용한다.
- 관측값에서 표본 평균을 뺀 뒤 표준편차로 나누어주면 표준화된 값을 구할 수 있다.
- 표준화된 값의 평균은 0, 표준화된 값의 표준편차는 1이다. ⇒ 즉 측정 단위에 영향을 받지 않게 중심위치와 척도 조정을 통해 절대비교 가능하다.


[참고자료]
datalink - coefficient of variation
https://www.datadata.link/qa03-3-2/
통계는에이스 - [최지민 박사의 통계 TV] 변동계수
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 자료를 파악하는 방법 (표, 그래프) (0) | 2022.08.15 |
|---|---|
| 기초통계 / 분포 형태를 나타내는 측도 (왜도, 첨도) (0) | 2022.08.14 |
| 기초통계 / 대표값 (평균, 중앙값, 절사평균, 최빈값) (0) | 2022.08.12 |
| 기초통계 / 자료의 종류, 척도의 종류 (0) | 2022.07.07 |
| 기초통계 / 모집단과 표본 (0) | 2022.07.07 |