💡통계 분석방법을 적절하기 선택하기 위해서는?
• 어떤 통계분석 방법을 선택할 지는 '자료의 속성/형태' 와 '분석 목적' 에 따라 달라진다.
• 즉, 분석하고자 하는 자료가 통계분석 방법에서 가정한 조건을 얼마나 만족하는지에 따라 분석 방법의 적절성이 결정된다.
변수의 자료 형태
| CASE | X | Y |
| 1️⃣ | 범주형 자료 | 범주형 자료 |
| 2️⃣ | 범주형 자료 | 수치형 자료 |
| 3️⃣ | 수치형 자료 | 범주형 자료 |
| 4️⃣ | 수치형 자료 | 수치형 자료 |
분석 목적
• 비교
- X(그룹)에 따라 Y에 차이가 있나요?
• 관계
- X와 Y가 관련이 있나요? (= X가 Y에 영향을 주나요?)
• 분류
- X에 따라 Y를 분류할 수 있나요?
- X, Y 를 함께 고려하여 비슷한 것끼리 묶을 수 있나요?
💡분석 목적마다 알맞은 '변수의 자료 형태'가 있다.
| 목적 | 의미 | 변수의 자료 형태 |
| 비교 | X(그룹)에 따라 Y에 차이가 있나요? | 1️⃣- 범주 그룹에 따라 빈도 or 비율에 차이가 있는지 |
| 2️⃣- 범주 그룹에 따라 평균 or 분산에 차이가 있는지 | ||
| 관계 | X와 Y가 관련이 있나요? | 4️⃣- X에 따라 Y가 어떻게 변하는지 |
| 분류 | X에 따라 Y를 분류할 수 있나요? | 3️⃣- X에 따라 범주 그룹으로 분류할 수 있는지 |
| X, Y 가 비슷한 것끼리 묶을 수 있나요? |
비교 & 1️⃣ X : 범주형 자료, Y : 범주형 자료
분할표(contingency table)
• 두 개 이상의 범주형 자료 변수를 동시에 고려하여 각각의 범주에 관측개체의 빈도를 정리한 교차표
• k개 범주형 변수에 대한 분할표를 ⇒ k차원 분할표라고 한다.
• 수치형 자료의 경우 순서형 자료로 범주화하여 분할표를 작성할 수 있다.
그래프
• 원도표(=파이 차트): 비교 그룹별로 파이 차트를 작성할 수 있다.
• 막대그래프(=바 차트): 분석 목적과 자료 형태에 맞게 빈도 or 비율을 선택하여 작성할 수 있다.
예시 1 범주형 변수 2개 ⇒ 2차원 분할표

예를 들어 남자 82명, 여자 78명을 대상으로 세 가지 비빔면 브랜드에 대해 선호도를 조사했다고 하자.
(1)분석 목적
세 가지 비빔면 브랜드에 대한 남여별로 선호도 차이가 있나요? '비교'
(2) 비율(= 상대도수)는 어떻게 나타낼까?
• 비율은 분석 목적 또는 자료가 어떻게 수집되었는지에 따라 다르게 계산될 수 있다 ★
• 해당 분석의 목적은 남여가 선호하는 브랜드가 다른지 비교하는 것이므로 분모를 각 성별 합계로 두는 것이 적절하다.
• 분모
☑ 성별 합계: (82, 78)
▢ 브랜드별 합계: (60, 62, 38)
▢ 전체 합계: (160)

• 브랜드별 합계를 분모로 두고 비율을 구하는 것은 해당 분석의 목적에서는 의미가 없다. 극단적인 예로 쉽게 이해해보자. 해당 예시에서는 조사대상 남여 성비가 비교적 비슷하게 구성되어 있지만 예를 들어 여자 조사대상이 훨씬 많은 상황이라고 생각해보자. (즉 여자의 빈도 수치 값에 전부 0이 하나 더 붙어있는 형태로 조사되었다고 치자.) 이 때 브랜드별 합계를 분모로 비율을 구하면 모든 브랜드에서 무조건 여자가 다 높은 비율을 갖게 될 것이다. 하지만 성별 합계를 분모로 하여 비율을 구하면 각 성별 안에서 어떤 브랜드를 선호하는지 알 수 있고 결국 우리의 분석 목적대로 성별에 따라 브랜드 선호도가 다른지 비교할 수 있게 된다.
• 해당 예시에서는 조사 대상이 몇 명인지 알고 시작했지만, 만약 무작위로 160명을 조사한 경우라면 전체 합계를 분모로 두고 비율을 구해야 한다. 이 경우 해석도 달라지게 된다. ⇒ 성별과 비빔면 브랜드 선호도 간 관련성 여부
예시 2 범주형 변수 3개⇒ 3차원 분할표

(1) 생존율 구하기
객실등급별 (%)
- 1등실: 202/325 = 62.2
- 2등실: 118/285 = 41.4
- 3등실: 178/706 = 25.2
- 승무원: 212/908 = 23.3
성별 (%)
- 남자: 338/(338+1352) = 20.0
- 여자: 316/(316+109) = 74.4
- 어린이: 56/(56+53) = 51.4
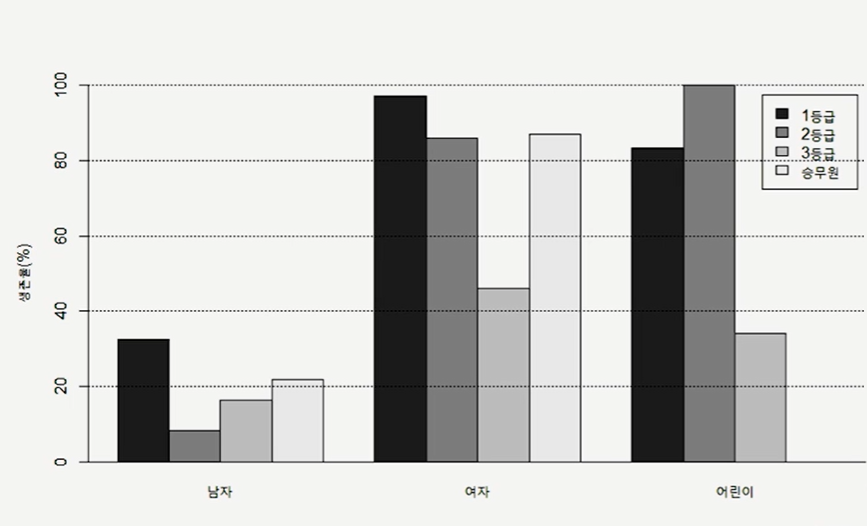
객실등급별 X 성별 (%)
| 남자 | 여자 | 어린이 | 전체 | |
| 1등실 | 32.6 | 97.2 | 83.3 | 62.2 |
| 2등실 | 8.3 | 86.0 | 100 | 41.4 |
| 3등실 | 16.2 | 46.1 | 34.2 | 25.2 |
| 승무원 | 21.7 | 87.0 | - | 23.3 |
| 전체 | 20.0 | 74.4 | 51.4 | 31.9 |
(2) 막대그래프
(3) 결과 해석
객실등급별만 봤을 때 승무원의 생존율이 가장 낮았지만, 성별 그룹안에서 객실등급별로 생존율을 확인하면 승무원의 생존율은 1등실을 제외한 나머지 등실의 승객보다 생존율이 높다. (*심슨스 패러독스)
(4) 이러한 결과가 나온 이유
승무원의 성비를 보면 남성의 비율이 압도적으로 높았기 때문이다.
| 남자 | 여자 | |
| 1등실 | 54.9 | 45.1 |
| 2등실 | 64.4 | 35.6 |
| 3등실 | 73.7 | 26.3 |
| 4등실 | 97.5 | 2.5 |
💡심슨스 패러독스
데이터의 세부 그룹별로 일정한 추세나 경향성이 나타나지만, 전체적으로 보면 그 추세가 사라지거나 반대 방향의 경향성을 나타내는 현상을 의미한다. 이 현상은 사회과학이나 의학 통계 연구에서 종종 발생한다
비교 & 2️⃣ X : 범주형 자료, Y : 수치형 자료
표
• 수치형 자료의 특성을 나타내는 값을 범주(그룹)별로 정리
• 수치형 자료의 특성을 나타내는 값 → 기본 통계값: 표본크기, 평균, 표준편차 등
그래프
• 점도표, 히스토그램(막대그래프)을 중첩, 병렬로 비교
• 동일 축 상의 그룹별 상자그림 비교
예시 범주형 변수 1개, 수치형 변수 1개

관계 & 4️⃣ X : 수치형 자료, Y : 수치형 자료
산점도(scatter plot)
각각의 관측 개체에 대해 두 변수의 값을 순서쌍으로 표현하고 2차원 평면상에 점으로 나타낸 그림.
산점도 행렬(scatter matrix)
3개 이상의 수치형 변수에 대해 두 변수씩 쌍으로 조합하여 산점도를 행렬 형태로 표시한 그림.
시계열 그림(Time series plot)
• 시계열 자료: 시간에 따라 수집된 자료로, 자료 간 종속성이 존재할 수 있어서 관측 순서가 중요하다.
• 시계열 그림: 시계열 자료를 x축에 관측 시점, y축에 관측된 값을 표시한여 나타낸 산점도
• 시계열 그림은 순서 파악을 쉽게 하기 위하여 일반적으로 관측 순으로 관측값들을 선으로 연결한다.
예시 수치형 변수 2개 (+ 범주형 변수 1개)

[참고자료]
위키백과 - 심슨의 역설 (https://ko.wikipedia.org/wiki/%EC%8B%AC%EC%8A%A8%EC%9D%98_%EC%97%AD%EC%84%A4)
'통계 노트 > 기초통계' 카테고리의 다른 글
| 기초통계 / 확률 변수, 확률 분포 (0) | 2022.08.16 |
|---|---|
| 기초통계 / 표본 공분산, 표본 상관계수 (0) | 2022.08.15 |
| 기초통계 / 분포 형태를 나타내는 측도 (왜도, 첨도) (0) | 2022.08.14 |
| 기초통계 / 산포도 (사분위범위, 표본 분산, 표본 표준편차, 변동계수) (0) | 2022.08.14 |
| 기초통계 / 대표값 (평균, 중앙값, 절사평균, 최빈값) (0) | 2022.08.12 |